

7

 |
 |
7 |
 |
|
The LA Fox Developer Newsletter
|
|
October 1999
|
|
Scheduling Concepts
(Con’t from page 1)
This type of problem is also encountered when a carpenter needs to cut pieces out of a sheet of plywood, or a tailor is cuthng pieces of cloth from a bolt of cloth. The container would be the plywood or bolt of cloth, respectively. Then instead of putting items into the container, you are taking them out, as parts of the container.
The
“Traveling Salesman” routing problem
The next class of scheduling problem is a routing problem
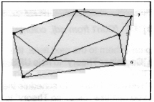
called the “Traveling Salesman Problem”. It assumes that a salesman must travel to a number of cities and return to the starting point. The goal is to have the salesman travel the least distance. This class of problem is called a “Network” problem. It is represented diagrammatically as a series of points called nodes, vertices, or points, joined by lines. This type of problem is encountered when scheduling the routing of mail carriers, freight carriers, etc. The lines do not have to represent physical distance; in some cases the lines represent the cost of travel or time of travel between the nodes.
In the above figure, point 1 is assumed to be home or the starting and stopping place.
At first glance, there is a tendency to try to solve this problem using total enumeration, by building a database table of all the distances between the cities and then creating a database table with all the possible combinations. The difficulty with this approach, as you can see below, is that the possible combinations can be very large.
The total combinations
=
T
Total number of cities
=
n
T=(n—1)!
Which means that in the above example with 7 cities there are 720 possible combinations. This is manageable with today’s computers; in fact, I wrote a FoxPro program to solve this through total enumeration just to serve as a check for other approaches. The shortest distance to travel to all of the cities was 28.533. But, this is a small problem; it doesn’t take too many additional nodes or cities to overwhelm even the largest computers.
|
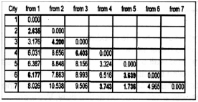
The most common approach to solving this problem is to find “local solutions” first, find the cities that are closest and connect those cities. Then, proceed from the “local solutions” to a general solution. There is a table of the distances between the cities below to help you. The closest cities are 5 & 7, then 1 & 2. As it turns out, they are part of the optimal solution. The next closest cities are 1 & 3; they are not part of the optimal solution. So, one has to be careful not to assume too much with this approach. My approach is to only use the closest 25% and then test combinations that include those solutions. You can assume that the shortest distance to travel would be a solution where the salesman does not travel to a city past another city. So, the solution above could be manageable, if a database table
of distances between cities were used and
if it were indexed by distance from the starting city each time you wanted to evaluate the next node. This approach can greatly reduce the combinations to be evaluated.
Below is a
table of
the distances between cities with the optimum solution in bold type:
"Waiting Line or Queuing” Problems
Waiting line or queuing
problems are encountered when we
need to
schedule personnel for a shift at work or for the rotation
of duties in a club or to schedule a machine on the shop floor. I have written a number of FoxPro programs to solve these types of problems. The following are two examples:
A few years ago, I was a member of a Toastmasters speaking
club. All of the members would rotate through duties each week with the primary assignment being the need for two speakers each week. When I was assigned the duty of creating the weekly schedules, I knew that I had to automate the task. It took a several hours each week to create the schedules manually with a spread sheet.
|
|
Page 7
|

 |
 |
7 |
 |